What Is Superposition in Neural Networks?
A Beginner’s Guide to How AI Packs More Features Than Neurons—And Why It Matters
Imagine trying to describe the entire world using only a handful of words. That's the challenge neural networks face, and superposition is their ingenious solution.
A note on ‘features’
Whilst we don’t fully understand how neural networks ‘think’, we’ve observed the emergence of features - distinct characteristic detectors which, if mapped out completely, provide a conceptual explanation for how neural nets work. Think of features as specific patterns or characteristics the network learns to recognise in its input data, like edges, textures, or even higher-level concepts like 'dog-ness'1.
The Problem
It would make it much easier for us to understand neural networks if these features were represented by individual neurons. Having our features each being assigned to individual neurons would not only make our job trying to understand the network easier, it would often make things slightly easier for the neural net itself2.
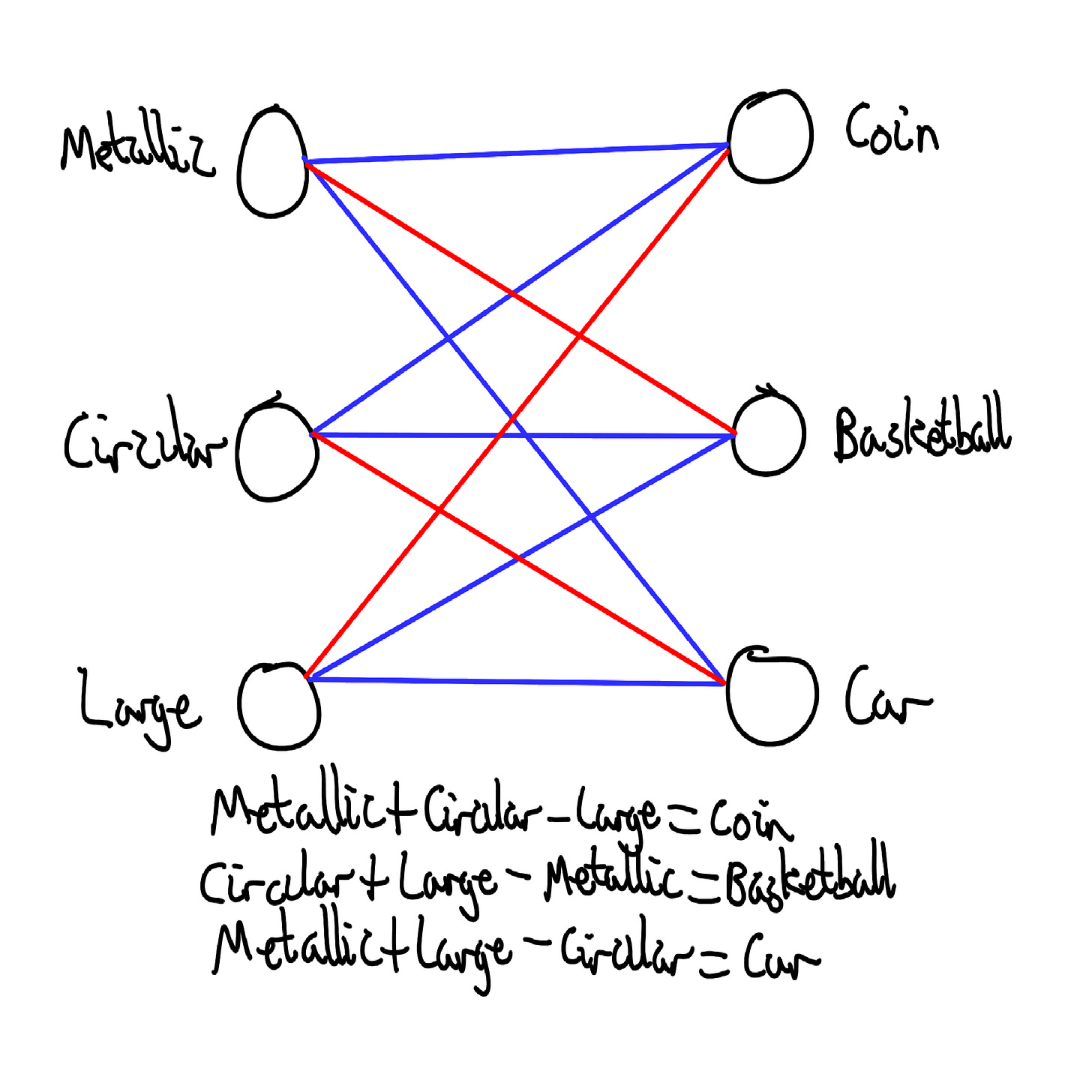
As you can see, this is not going to work. What defines ‘large’? How ‘circular’ does our input need to be not to be a car? Try as you might, it’s not going to work without a lot of features for all the scenarios we encounter in messy real-world data. Put another way:
As you can see, there are practically infinite features which would be helpful for our neural network to classify stuff (or make stuff relevant to prompts, for generative models). Because of the variety of real world data, this extra detail is almost always more useful to the model than the drawbacks, so the model ends up with many more features than available neurons to fit them in individually.
To solve this problem, neural networks use a clever trick called superposition.
How Superposition Works
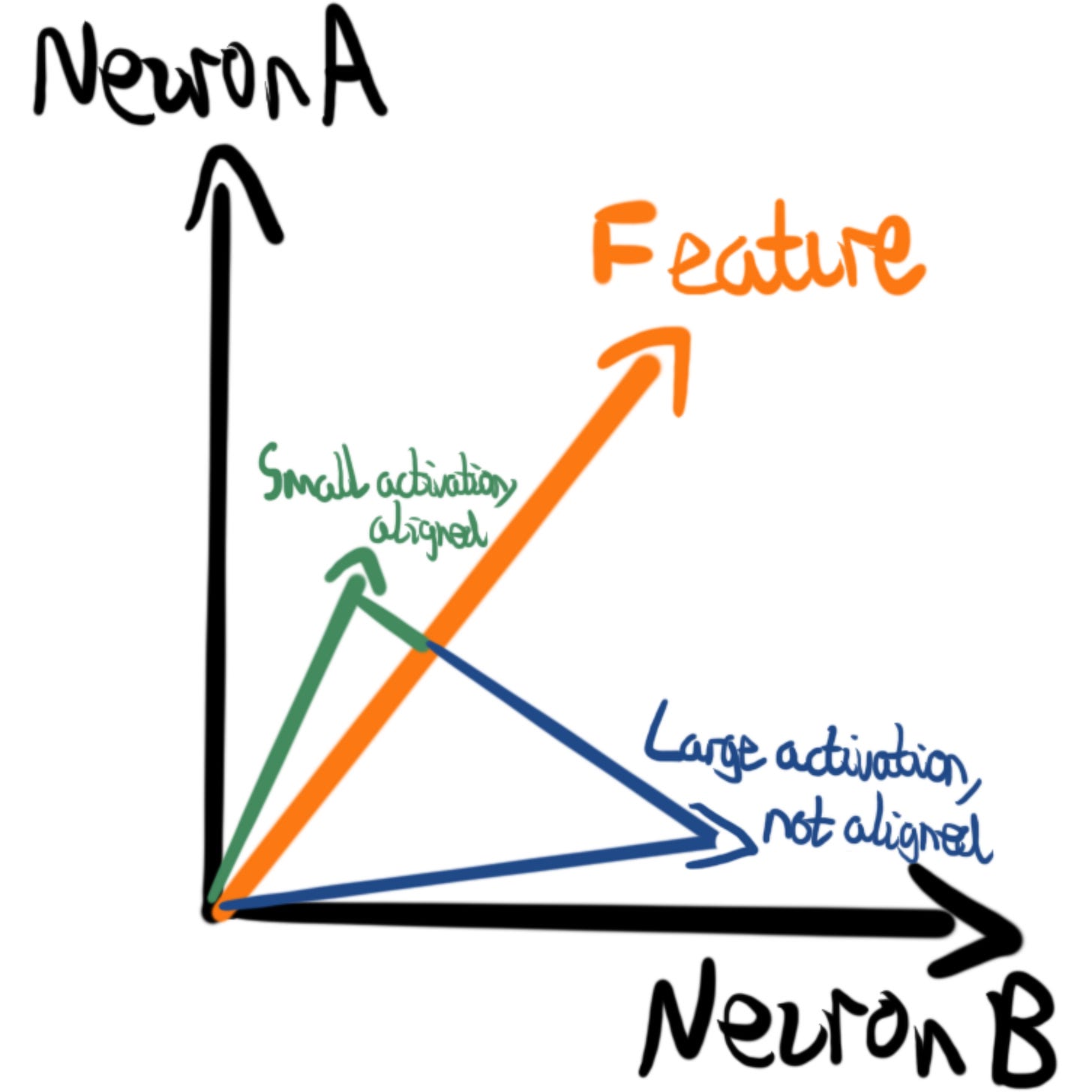
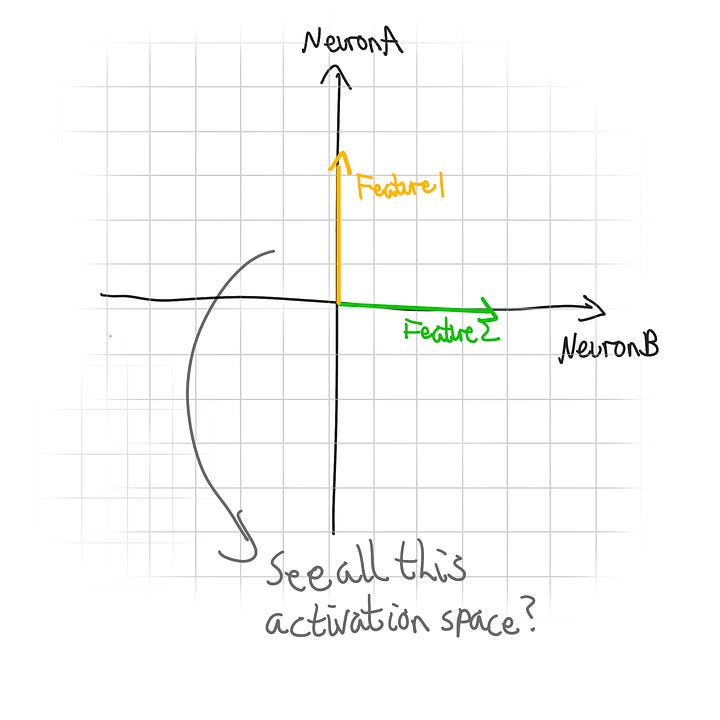
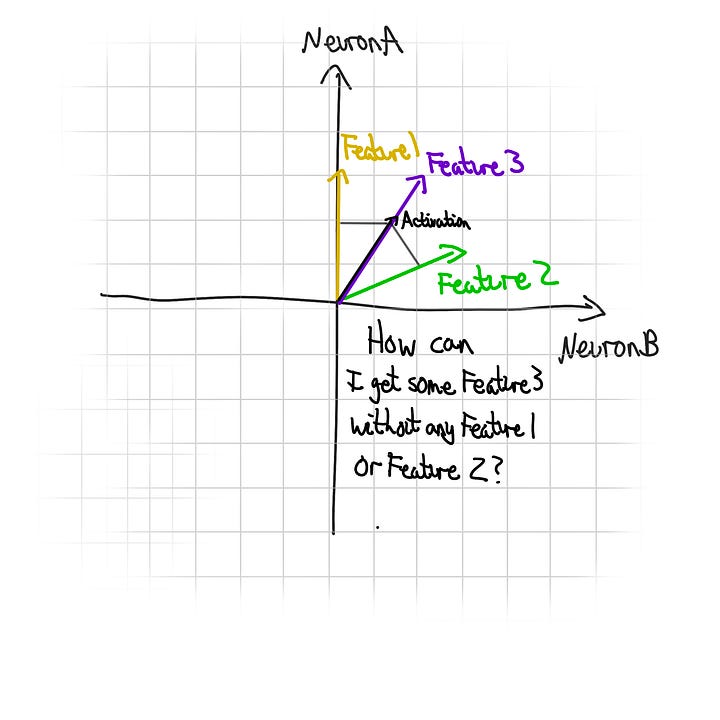
In order to fit these extra features into those neurons, the model will represent the features as ratios of neuron activations. This is commonly described as directions in the activation space3. This concept can be challenging to grasp initially, but here's a concrete way to think about it4:
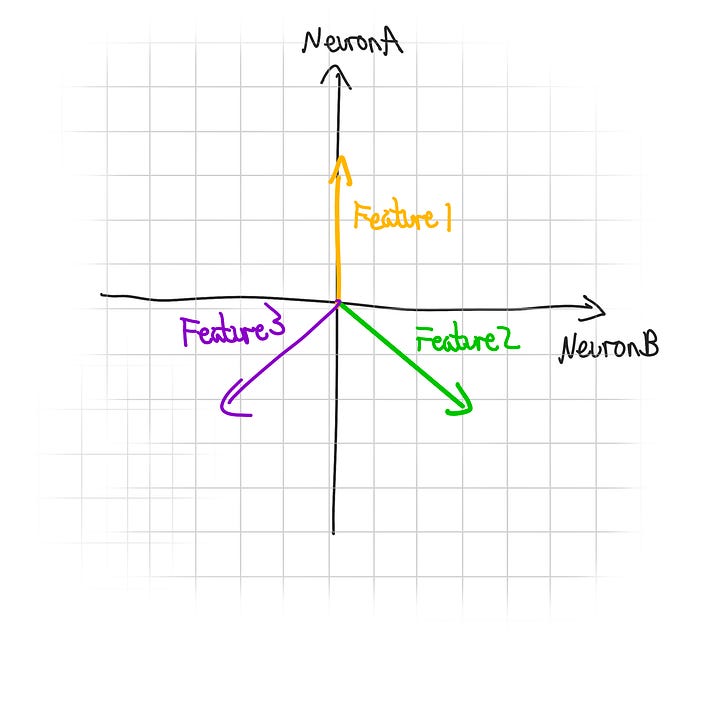
How strong our feature is being represented can be found by seeing how aligned our activation is with that ratio, and how large our activation is in total5.
This is also why the neural net spaces features as far apart as possible (see earlier diagram). If features are too close together, activations will cause multiple features to be engaged (known as interference).

A great way to think about this is paint colours. We want to represent many items with different colours, but we only have a limited number of paints. We can mix paints together to get different shades, so we can represent more items. However, if we make them too close in colour, we could get them muddled up.
Just like mixing paint allows us to create more shades, superposition allows for many more concepts to be represented within a finite range of activation ‘colours’, with the trade-off that concepts become harder to distinguish.
The trouble with superposing multiple features per neuron for the model is that the model itself doesn't know what feature has caused previous neurons to fire.
Therefore, during training the model naturally ensures that features that are unlikely to be seen together are superposed onto the same neurons. This minimises the confusion.
An example
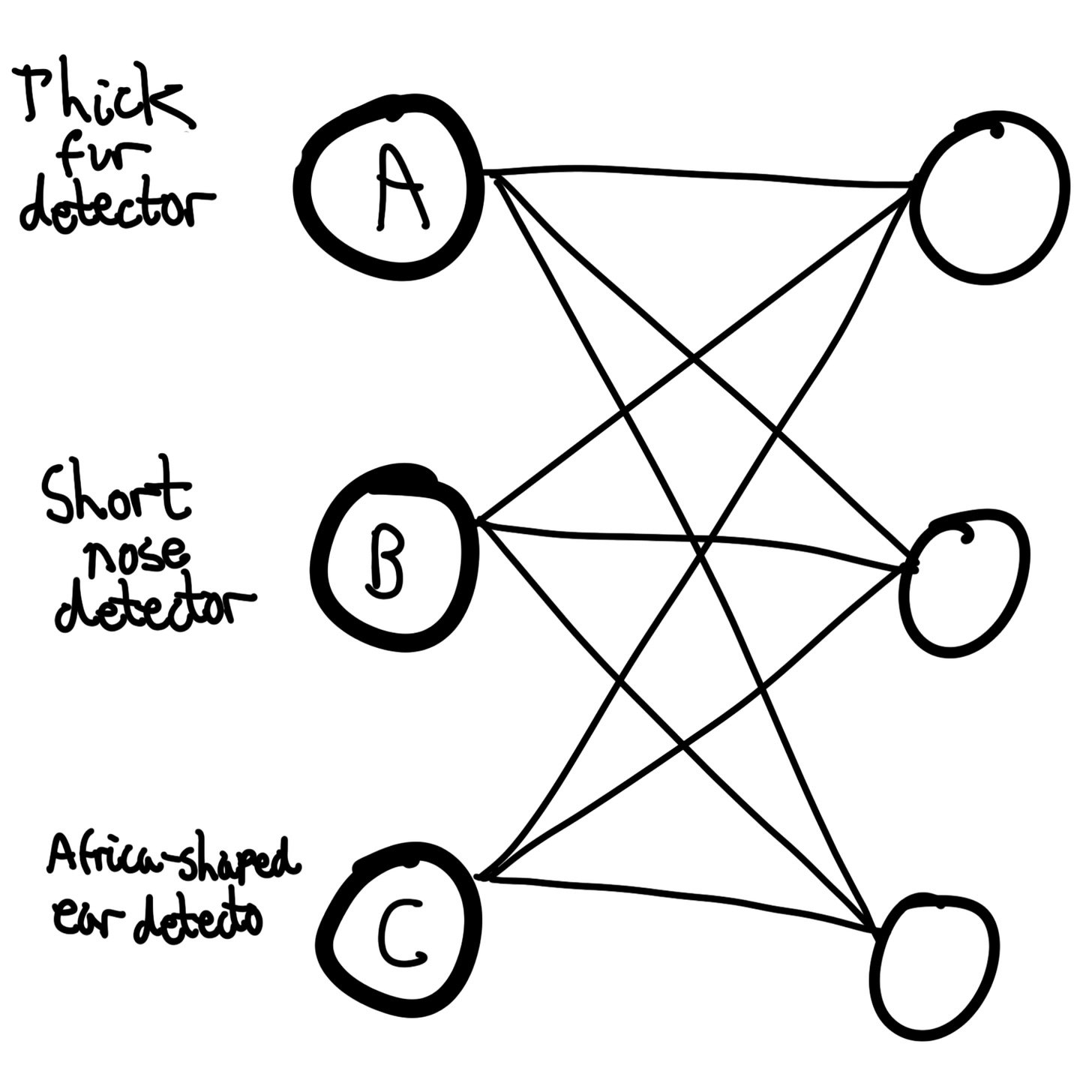
Suppose we have a neural net which identifies different types of dogs and different types of elephant6:
Since neurons A and B alone are enough to determine the subject is a dog, the network can afford to repurpose Neuron C for a different feature when those conditions hold. This means we could let C also represent a dog feature (e.g. small dog detector).
Why superposition makes understanding neural nets so hard
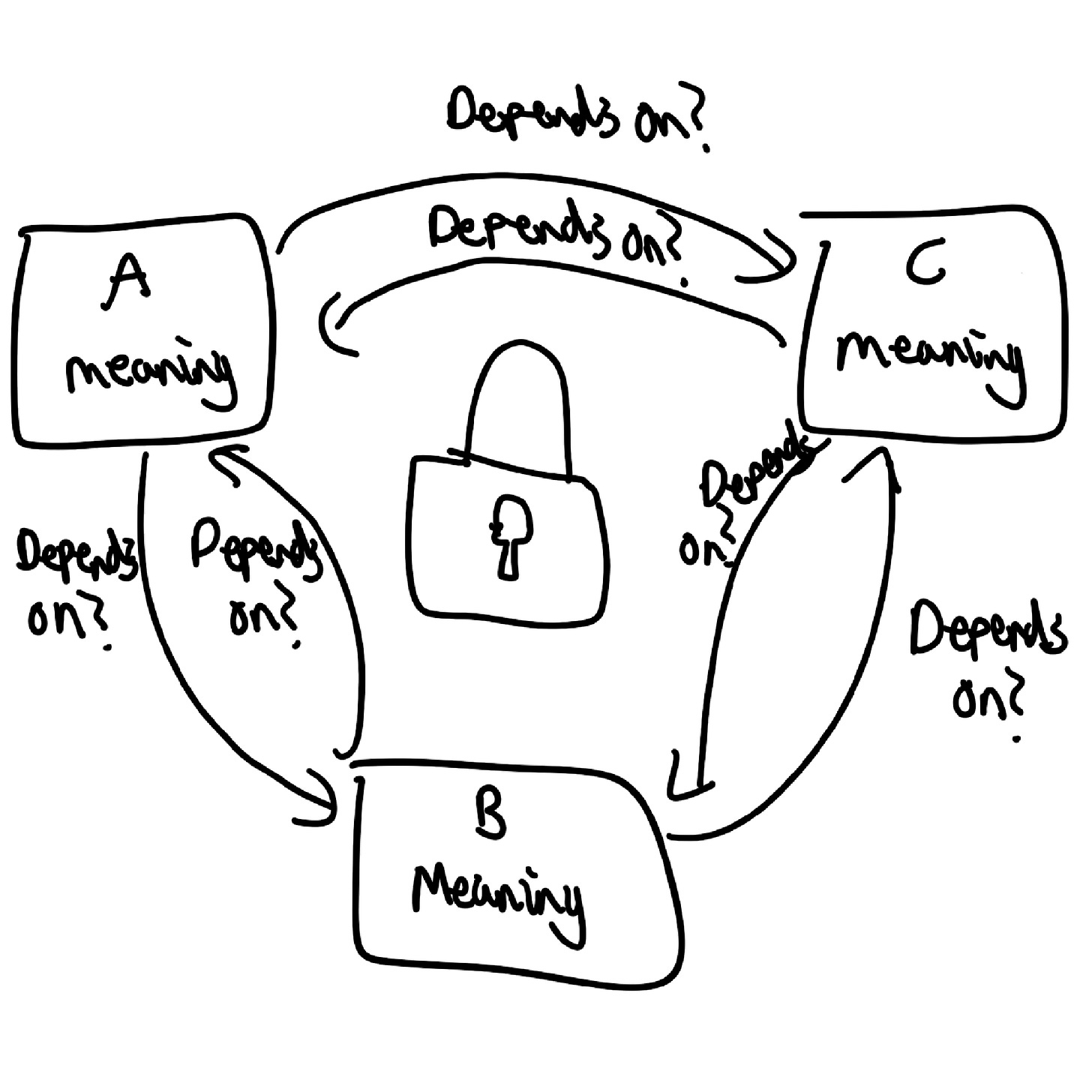
In other words, Neuron C will activate for entirely different features, and we won't be able to identify what has caused it to activate without looking at the other neuron activations, and also knowing what those activations mean.
If neurons A and B also have superposed features for different contexts, this creates a knot of combinations which is very difficult to pick into.
Now remember that most features are expressed as ratios of neuron activations (and not necessarily of the neurons next to each other). Isolating individual features requires analysing the network’s entire activation space, which is nearly impossible for large networks using today’s methods.
This is an extremely pressing problem; Because features are hidden in these tangled combinations, it makes it incredibly difficult to understand the reason a model might have made a decision, and makes larger models inherently more unpredictable. This lack of transparency is a key challenge for AI safety.
Summary
We’ve observed clear features in neural networks.
There are many more features than neurons.
In order to represent all these features with the limited number of neurons, the network represents features as ratios of neuron activations, or more concretely directions in the activation space.
The challenge this creates is interference. In order to minimise this, the model spreads features out as far apart as possible, and ensures that features which are unlikely to be seen together occupy the same sets of neurons.
Final thoughts
Superposition is not just a byproduct of how neural networks train; It’s one of the fundamental reasons they’re so powerful. If we’re going to make neural networks interpretable, which appears to be one of the most promising pathways in AI Safety, methods of effectively disentangling superposed features is critical7.
As far as I’m aware, superposition as an area of study wasn’t even a thing until around 2018. Since then, it has rapidly become one of the most tractably impactful tranches of mechanical interpretability and possibly even AI Safety as a whole, particularly the work done by the team at Anthropic (to further understand superposition at a mathematical level, I really recommend reading Toy Models of Superposition).
I think work on this is currently most suited to those with a strong mathematical or computer science background, but I expect as the field matures it will become extremely interdisciplinary (after all, superposition is all about drawing connections between things).
Finally, I would love to get critique on this work. There are so many times through this where I’ve realised my understanding was entirely wrong and have had to virtually rewrite. I’m hoping this explainer will help ‘bridge that gap’ so it’s just a little bit easier for the next person to learn.
Some resources I recommend:
There's a huge amount of debate for what defines a 'feature' (and if features are really ‘a thing’). I consider features to be learned representations of patterns in the data, which can range from low-level (edges, textures) to high-level (concepts like 'dog-ness'). This explainer would work for most other definitions of features, so long as those definitions recognise: 1. That features exist. 2. That there are many more features than neurons in a neural network. 3. That many features can be active at once.
Activation functions encourage features to align with individual neurons because they can change the ratio of outputs. This is especially true for the sigmoid function (as it’s very sensitive to change for middle values), but still applies somewhat to ReLU and other modern activation functions.
The activation space is the range of all possible neuron activations. ML researchers like to think about it as a multidimensional space where the possible activations of each neuron represent a dimension. It sounds way more complicated than it is, especially if you think about it in terms of only 2 or 3 neurons (either a 2D or 3D graph).
A note on negatives. Yes we can't have a negative activation of a neuron (for most activation functions). However, by using negative weights we can effectively make the activations appear negative at the receiving neuron. That being said, the centre of geometry is not usually at the actual origin; I just did it for simplicity.
For those who know linear algebra: this is the dot product.
It goes without saying that this is a massive oversimplification.
There are researchers who argue that either features aren’t a good way of modelling neural networks or that mech interp isn’t the best path for AI Safety. However, they are in the minority.